Problèmes de logique : les solutions

1. Les comédiens

« joue le rôle de »	Roi	Soldat	Fou	Bourreau	Prisonnier
Antoine	x	o	x	x	x
Bruno	o	x	x	x	x
Charles	x	x	x	x	o
Denis	x	x	o	x	x
Etienne	x	x	x	o	x

2. Les métiers

	Peintre	Maçon	Menuisier
M. Peintre	o	x	x
M. Maçon	x	o	x
M. Menuisier	x	x	o

3. Les couples à la plage

	Barbara	Isabelle	Geneviève	Gisèle	Nadine
Rémi	x	o	x	x	x
Nicolas	o	x	x	x	x
Jacques	x	x	x	x	o
Thomas	x	x	o	x	x
Robert	x	x	x	o	x

4. Le trio

Si Alexis est à la guitare, Charlie devrait être à la fois au piano et à la guitare : impossible.

	Guitare	Piano	Batterie
Alexis	O
Bruno	O
Charlie	O	O

Si Alexis est au piano, Bruno et Charlie sont à la guitare.

	Guitare	Piano	Batterie
Alexis		O
Bruno	O
Charlie	O

Si Alexis est à la batterie, Charlie devrait être à la fois au piano et à la guitare : impossible.

	Guitare	Piano	Batterie
Alexis			O
Bruno	O
Charlie	O	O

Dans tous les cas, aucun ne peut jouer de la batterie sans violer la règle.

5. Les maisons

Le poisson appartient à l'Allemand:

jaune	bleue	rouge	verte	blanche
Norvégien	Danois	Britannique	Allemand	Suédois
Dunhill	Blend	Pall Mall	Prince	Gauloises
chats	chevaux	oiseaux	poisson	chien
eau	thé	lait	café	bière

6. Les voyageuses

	Californie	Texas	Floride	Arizona
Louise	o	x	x	x
Martine	x	o	x	x
Carole	x	x	o	x
Henriette	x	x	x	o

	Lion	Tigre	Zèbre	Poulain
Louise	x	x	o	x
Martine	x	o	x	x
Carole	x	x	x	o
Henriette	o	x	x	x

7. Les professeurs

	Français	Anglais	Histoire	Latin	Mathématiques	Économie
Mme Arthur	x	x	x	x	o	x
Melle Blais	x	x	o	x	x	x
Mme Côté	o	x	x	x	x	x
M. Duval	x	x	x	x	x	o
M. Élie	x	o	x	x	x	x
M. Ferron	x	x	x	o	x	x

8. La fête des enfants

La plus sympathique, en brun, est en conséquence Solange.

	vert	jaune	rouge	brun	bleu
Berthe	X	X	X	X	O
Edith	X	X	O	X	X
Marguerite	O	X	X	X	X
Solange	X	X	X	O	X
Jeannine	X	O	X	X	X

9. La plage

	Lucien	Daniel	Roland	Bernard	Denis
Catherine	x	o	x	x	x
Diane	x	x	o	x	x
Peggy	x	x	x	o	x
Michelle	x	x	x	x	o
Maureen	o	x	x	x	x

10. Le goûter

	Orange	Brioche	Pomme	Pain chocolat	Pain raisin
Michelle	x	o	x	x	x
Irène	x	x	x	x	o
Pierre	x	x	o	x	x
Sarah	o	x	x	x	x
Nicolas	x	x	x	o	x

11. Les époux

	Alain	Serge	Marc
Lise	x	o	x
Monique	x	x	o
Hélène	o	x	x

12. Le club des trois

	Trésorier	secrétaire	président
Michel	o	x	x
Louis	x	o	x
Lisette	x	x	o

13. Les enseignants

	Anglais	Français	Maths	Histoire	Géographie
Lenoir	o	o	x	o	x
Leblanc	x	x	o	o	o
Leroux	o	o	o	x	x

14. Les cadeaux

	Scooter	Gilet	Baladeur	Ordinateur	Radio
Marie	x	o	x	x	x
Suzie	o	x	x	x	x
Julie	x	x	o	x	x
Brigitte	x	x	x	x	o
Martine	x	x	x	o	x

Les cravates *

Messieurs Lenoir, Lebrun et Levert mangeaient ensemble au restaurant.

Tous portaient des cravates de couleur.

L'un portait une cravate noire, l' autre portait une cravate brune et le dernier portait une cravate verte.

Soudain l'homme portant la cravate verte s'écria : "Réalisez -vous que chacun porte une cravate de la même couleur que nos noms mais personne ne porte une cravate semblable à son nom."

"C'est curieux", s`exclama monsieur Lenoir.

Quelle couleur de cravate portait chaque homme ?

	Noire	Brune	Verte
Lenoir	X	O	X
Lebrun	X	X	O
Levert	O	X	X

Fréquentation *

Anne a les cheveux blonds, Josée a les cheveux roux et Claire a les cheveux bruns.

Elles fréquentent Denis, Aurel et Jacques.

Claire n' aime pas Denis.
Josée fréquente le frère de Denis.
Jacques fréquente la sœur de Josée.

Qui fréquente qui ?

	Anne	Josée	Claire
Denis	O	X	X
Aurel	X	O	X
Jacques	X	X	O

Couples (2)

	Laure	Arlette	Marie
Éric	x	o	x
Aurélien	x	x	o
Antoine	o	x	x

15. Démarrer du pied gauche

Jamais. Tous les deux cycles, leurs pieds droits sont synchrones, mais jamais leurs pieds gauches. 

16. Traversée en famille

1. Les deux garçons traversent ensemble. L’un deux revient seul sur la première rive.
2. La mère traverse seul et le 2^e fils ramène la barque.
3. Les deux garçons traversent ensemble de nouveau et l’un d’eux revient seul.
4. Le père traverse à son tour. Le garçon qui attendait avec sa mère ramène la barque de l’autre côté.
5. Les deux fils traversent ensemble et rejoignent leurs parents.

17. Le reflet

Votre reflet tient la lettre « b » dans la main droite.

18. Chez les Menteurs (1)

C’est impossible : un Franc ne dira jamais qu’il est un Menteur, et un Menteur non plus .

19. Chez les Menteurs (2)

Comme on vient de le voir, un Menteur ne prononcera jamais « Je suis un menteur » . Celui qui répond a menti, et le premier est donc un Franc.

20. Chez les Menteurs (3)

Même chose encore : un Menteur ne peut avouer appartenir à un groupe de Menteurs. Cette affirmation est fausse. Le deuxième dit peut-être la vérité, peut-être un mensonge. On ne peut le savoir. Mais dans les deux cas, le troisième est un Franc.

21. Les deux gardes

Si le garde interrogé dit la vérité, il rapportera le mensonge que profèrerait son collègue. S’il dit faux, il indiquera là aussi la mauvaise porte. Dans les deux cas, il faudra prendre l’autre porte, la bleue.

22. Le choix impossible

Il ne pourra être pendu, car sinon il aura dit vrai et devra être décapité. Mais alors il aura menti et sera pendu, ce qui est impossible… Mieux vaut le libérer !

23. Les trois coffrets

-         si c’est celle du coffre en or, la deuxième est vraie aussi, ce qui est impossible.

-         Si c’est celle du coffre d’argent, le portrait ne peut être ni dans le coffre de plomb car son affirmation serait vraie aussi, ni dans le coffre d’or pour la même raison.

-         L’affirmation du coffret de plomb peut être la seule vraie si on place le portrait dans le coffre d’argent : alors les deux autres inscriptions sont bien erronées.

24. La pièce disparue

Tout dépend comment on présente le problème. Le patron a bien empoché 25 €, le garçon a gardé 2 € et les hommes ont récupéré 3 €. Cela correspond bien aux 30 €. Il ne faut pas ajouter 27 + 2, mais plutôt 25 + 2 + 3.

25. Suite de lettres

N, comme Novembre. Ce sont les initiales des mois de l'année.

26. Les trois chats

Les mêmes trois chats. Trois chats prennent en moyenne une souris à la minute.

27. Reproduction de méduses

L'aquarium sera à moitié rempli une minute avant deux heures, soit à 13 h 59.

28. Rencontres à l’heure

Elles se croisent 11 fois si on ne compte pas douze heures deux fois :

1. 12 h 00
2. 1 h 05
3. 2 h 10
4. 3 h 16
5. 4 h 21
6. 5 h 27
7. 6 h 32
8. 7 h 38
9. 8 h 43
10. 9 h 49
11. 10 h 54

29. Combien de fois 9 ?

Vingt fois. De 1 à 100, le 9 est utilisé dix fois comme unité (9,19,29,39,...), et dix fois comme dizaine (90, 91, 92,...).

30. Les chaussettes (1)

Il en prend trois.

31. Les chaussettes (2)

Il sera obligé d'en prendre 26 : dans le pire des cas, il pourrait choisir les 24 chaussettes bleues.

32. Les hommes de couleur

Monsieur Lerouge ne porte pas de costume rouge. Puisqu’il répond à l'homme au costume bleu, il est donc habillé de vert. L'homme au costume bleu est donc que M. Levert ; M. Lebleu est vêtu de rouge.

33. Lettres particulières

Le Z devrait se retrouver sur la ligne avec toutes les autres lettres constituées uniquement de segments de droite.

34. Le train dans le tunnel

Il lui faudra deux minutes : une minute pour y rentrer complètement, une autre minute pour en sortir complètement.

35. L’échelle du navire

Toujours neuf, car le navire et l'échelle monteront en même temps que la marée.

36. Les deux cordes à brûler

Notons A et B les extrémités de la 1ère corde et C et D les extrémités de la deuxième. Il suffit d'allumer A, B et C en même temps. Lorsque la 1ère corde a complètement brûlé, il s'est écoulé 30 minutes. On allume alors l’extrémité D : la demi-heure restante sur la deuxième corde est divisée en deux et brûle en 15 minutes.  30 + 15 = 45 minutes.

37. Tour de nombres

La suite se lit ainsi :

Un

Un 1

Deux 1

Un 2, un 1

Un 1, un 2, deux 1

Etc.

La suite sera

1113213211

38. Qui est l’aîné ?

Sophie > Tom > Anne

Sophie !

39. Les trois interrupteurs

On allume quelques secondes le premier interrupteur, puis on l'éteint. On allume le second et on va dans la pièce à côté. Si la lumière est allumée c'était le deuxième, si l'ampoule est éteinte mais chaude c'était le premier, si elle est froide c'est le troisième.

40. Rangement de nombres

7, puisque les nombres sont rangés dans l’ordre alphabétique :

cinq, deux, huit, neuf, quatre…

41. Les mots de passe
Vous répondez « 4 », le nombre de lettres du chiffre 7.

42. Le monastère
On se place donc dans la tête d'un moine atteint (puisqu'il existe) : s'il ne voit personne atteint lors de la prière du soir, il va en déduire que lui est atteint, donc se suicider le soir même. Un deuxième moine atteint, s'il le voit atteint le premier jour, et encore vivant le lendemain, en déduit que le 1° moine atteint en a vu un autre. C'est forcément ce second moine, qui se sait atteint. Donc si exactement 2 moines sont atteints, ils se suicident tous deux le 2° jour. On raisonne par récurrence : (c'est mieux que le problème, on va résoudre au n° jour) On se place dans la tête du n° moine atteint, qui en a vu n-1 atteints les autres jours. S'ils sont encore vivants au n° jour, c'est qu'ils ne sont pas n-1 atteints. Le n° moine se sait alors atteint, et les n moines atteints par la malédiction se suicident le n° jour. Dans le problème posé, tous les moines maudits se suicident le soir du 7° jour. Donc exactement 7 moines étaient atteints.

43. Les deux gants
L'homme met les deux gants, l'un sur l'autre, il serre la main du premier extra-terrestre. Il retire le gant du dessus et serre la main du deuxième extra-terrestre. Ensuite, il remet le gant du dessus mais dans l'autre sens (les deux faces contaminées sont l'une sur l'autre) et il serre la main du troisième extra-terrestre.

44. Le chat Bichou

Il faut simplement démêler les affirmations :

3 Bichou n’a pas de panier.

7 S’il n’a pas de panier, Bichou est roux.

2 montre que Bichou est rusé.

5 s’il est rusé, il est du quartier.

1 s’il est du quartier, il mange dans le plat de mon chien.

6 Bichou est compagnon d’errance.

4 S’il est compagnon d’errance, Bichou aime les os à moelle.

45. Les cent déclarations

Chaque affirmation reniant toutes les autres, ou bien une seule est vraie, ou bien aucune n'est vraie.

1re hypothèse: Une seule déclaration est vraie.

Seule la 99e, en affirmant qu'il y a 99 affirmations fausses, nous affirme qu'il n'y en a qu'une de vraie.
S'il y en a une, c'est obligatoirement la 99^e.

2e hypothèse: Aucune déclaration n'est vraie.

Elles sont donc toutes fausses. La 100e déclaration affirmant la même chose serait donc vraie.
Il y a contradiction. Hypothèse non confirmée.

Conclusion: Une seule déclaration est vraie et c'est la 99e. Toutes les autres sont fausses.

46. Le fou et l'asile

Le fou peut revenir sur ses pas vers sa propre chambre, car aucun cadavre ne s'y trouve. Cette petite boucle lui permet de visiter une seule fois chacune des chambres des autres malheureux internés pour y commettre ses horribles crimes et donc de s'enfuir...Gare à vous!

47. Le monstre
Le monstre fait 60 mètres de long.

48. Le professeur généreux

« Vous n’allez pas me donner  1 € »

Ou « Vous  allez me donner 50 € ou rien. »

49. Le tyran tricheur

La jeune fille prit l’un des cailloux, le jeta au loin en disant « J’ai choisi celui-ci. Montre-moi maintenant celui que je refuse ».

50. Les trois sports

Celui qui ne joue pas au tennis ne joue pas à la pétanque et, aussi, ne joue pas au golf. (Le 'non-pétanquiste' doit être le même dans les deux cas, sinon il y a contradiction avec les données qui affirment que deux jouent à la pétanque.)

Donc, il ne joue à aucun des trois sports.

Ainsi, chacun des deux autres amis pratique les trois sports.

51. Le nénuphar

29 jours !

52. L’âge des amis

indice 1	indice 2	indice 3	indice 4	indice 5	solution
Rose Thomas Guillaume Robert	Suzanne Rose Robert	Jean Robert	Jean Suzanne Rose	Jean Thomas	Jean Suzanne Rose Thomas Guillaume Robert

C'est Jean qui est le plus vieux des six amis.

53. La famille de Jeanne

Il y a quatre filles et trois garçons dans la famille de Jeanne.

On trouve la réponse empiriquement ou par l’algèbre :

Pour Jeanne, le nombre de sœurs est égal au nombre de frères:
Filles – Jeanne = Sœurs = Garçons
F-1 = S = G
F = G+1

Pour Roland, le nombre de sœurs est le double du nombre de frères:
Filles = Sœurs = 2 x Frères = 2 x (Garçons - Roland)
F = S = 2x(G-1)

Ainsi, en combinant l'équation de Jeanne avec celle de Roland:
G+1 = 2x(G-1)
G+1 = 2G-2
1+2 = 2G-G
3 = G -- il y a trois garçons

Et, en substituant la valeur de G dans l'équation de Jeanne:
F = G+1
F = 3+1
F = 4 -- il y a quatre filles

54. La couleur sur le front

Puisque les trois hommes ont levé la main, le vainqueur a compris qu’il ne pouvait y avoir que deux possibilités : soit deux marques bleues et une rouge, soit trois bleues.

Si l’un d’entre eux avait une marque rouge, les deux autres verraient chacun une marque bleue et une rouge ; auraient-ils une marque rouge eux aussi ? Dans ce cas, l’un d’eux n’aurait pas levé la main, apercevant deux marques rouges. Si les trois lèvent la main, il n’y a donc pas deux marques rouges.

Le vainqueur s’est dit : « Si j’avais une marque rouge sur le front, l’un des deux autres en aurait immédiatement déduit que son front ne pouvait être marqué de rouge. Puisque personne ne peut en déduire sa couleur, c’est donc que les trois marques sont bleues ». 

55. La moitié de la hauteur

Elle mesure 1,60 m.

56. Vente et revente

Il a fait 200 € de bénéfice car il a réalisé un profit de 100 € chaque fois qu’il a revendu la voiture.

57. Suite de lettres

N X S E Q X T T

Pourquoi? uN, deuX, troiS, ...

58. Le marché

Quelle est la règle pour déterminer ce qui se vend au marché ?

"Pas d'i, pas d'o" dans le nom d'un produit qui s'y trouve...

Mon premier a des plumes, pas de poil.

Mon second a des poils, pas de plumes.

Mon troisième contient quelquefois des plumes et des poils.

Mon quatrième a des poils, pas de plumes.

Mon tout n'a ni plume, ni poil.

59. Les chameaux

Abdullah ne possède aucun chameau.

Un seul énoncé doit être vrai. Si le premier énoncé est vrai, le dernier l’est aussi. Si le second énoncé est vrai, le troisième peut l’être aussi, sauf si le nombre de chameau est inférieur à 1.

60. Suite géométrique

C’est la figure

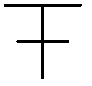
Il s’agit des lettres A, B, C, D, E représentées en symétrie, comme si le coté gauche était leur reflet dans un miroir.

61. Traversée de la rivière

Solution possible :

1. Mathurin traverse la rivière avec le lapin ; le renard et la salade  restent sur la berge.
2. Il revient chercher la salade, la pose à la place du lapin et ramène celui-ci avec lui.
3. Il dépose le lapin, prend le renard et va le poser à côté de la salade.
4. Il revient chercher le lapin et traverse une dernière fois la rivière.

62. Le fils de Joseph

Il suffit de remplacer « le père de mon fils » par « moi » pour comprendre que Joseph est mon père. Je suis donc un homme.

63. La mère de Joseph

Cette fois, Joseph est mon fils ; je suis sa mère.

64. Soixante flèches

A 12 h 59.

65. La revanche des cent mètres

Carl perdra à nouveau. Quand il atteindra 90 mètres, Ben aura parcouru cent mètres et ils seront à la même hauteur. Les dix derniers mètres seront remportés par le plus rapide des deux, c’est-à-dire Ben.

66. Série de nombres

Quatorze : chacun des nombres a une lettre de plus que celui qui précède.

67. Série de lettres

H, l’initiale de huit. Les autres lettres sont les initiales de un, deux, trois, quatre…

68. Pièces en croix

Il faut prendre la dernière pièce de la rangée de six et la poser sur la pièce à l’intersection des deux rangées.

69. Défilé de canards

Trois canards marchant en file indienne.

70. Le poids des canettes

Un quart de livre. La solution est très simple si on retire une canette de chaque plateau. On se retrouve alors avec deux canettes d’un côté et une demi-livre de l’autre.

71. Famille nombreuse

Les six filles ont le même frère. Avec M. et Mme Martin, cela fait neuf.

72. Les chasseurs du village

Il y a 99 chasseurs et un habitant qui ne chasse pas.

73. La menteuse

Mathilde ne dira jamais qu’elle s’appelle ainsi, donc Véronique ne peut rapporter de telles paroles.

Véronique ne le dira jamais non plus, donc Mathilde peut prononcer ces paroles puisqu’il s’agit d’un mensonge.

74. A travers la Terre

Le caillou tomberait jusqu’au centre de la Terre, le dépasserait par la force de l’inertie, puis reviendrait vers le centre, en effectuant ce trajet comme une balle qui rebondit avant de s’immobiliser enfin en plein centre de la Terre.

75. Dix par cinq

Il faut les planter sous la forme d’une étoile à 5 branches.

76. La somme des 100

Le résultat est 5050. Geneviève a compris qu’additionner les nombres aux extrêmes de la série simplifie le calcul : 1+99=100, 2 +98=100, 3 +97=100, etc. Jusqu’à 49 +51=100, soit 49 fois 100. Cela donne 4900. Il reste à ajouter le chiffre du milieu et celui de la fin, 50 et 100, ce qui donne un total de 5050.

77. L’âge des trois filles

La première réponse permet d’obtenir 8 solutions possibles :

1 x 1 x 36

1 x 2 x 18

1 x 3 x 12

1 x 4 x 9

1 x 6 x 6

2 x 3 x 6

2 x 2 x 9

3 x 3 x 4

La deuxième réponse amène à calculer la somme des nombres dans chaque cas :

1 + 1 + 36 = 38

1 + 2 + 18 = 21

1 + 3 + 12 = 16

1 + 4 + 9 = 14

1 + 6 + 6 = 13

2 + 3 + 6 = 11

2 + 2 + 9 = 13

3 + 3 + 4 = 10

Si le premier homme est incapable de donner une réponse, c’est que nous sommes dans le cas où les deux résultats sont identiques :

1 + 6 + 6 = 13

2 + 2 + 9 = 13

La troisième réponse parle de l’aînée, donc l’âge des trois filles est 2 ans, 2 ans et 9 ans.

78. Le prix du bouchon

Mais non, le bouchon ne coûte pas 10 centimes ! Dans ce cas, le prix de la bouteille seule serait 2 + 0,10 = 2,10 €, or la bouteille PLUS le bouchon coûtent 2,10 €.

Le prix du bouchon est 5 centimes, et celui de la bouteille 2,05 €.

79. Les cartes

Roi de carreau, valet de cœur, dame de pique.

80. Les fils de Barnabé

8, 12 et 16 ans.

81. Les chèvres

5 et 7 chèvres.